วัตถุที่เคลื่อนที่อยู่ในอวกาศนั้นอาศัยแรงเฉื่อยในการเคลื่อนที่ (เว้นแต่มีแรงขับ) ซึ่งเป็นไปตามกฏข้อที่ 1 ของนิวตัน เรียกว่า กฏของความเฉื่อย แต่เมื่อวัตถุนั้นเคลื่อนที่เข้าใกล้วัตถุที่มีขนาดใหญ่กว่า แรงโน้มถ่วงของวัตถุที่มีขนาดใหญ่กว่าจะดึงให้วัตถุที่มีขนาดเล็กเคลื่อนที่เข้าหาโดยมีทิศทางที่เบี่ยงเบนไปจากแนวการเคลื่อนที่เดิม จะเรียกว่าแรงโน้มถ่วงอื่นๆในอวกาศ เป็นแรงที่คอยรบกวนการเคลื่อนที่ในอวกาศก็ได้ครับ
ซึ่งในบริบทของ ดาวเทียมที่โคจรอยู่รอบโลก แรงโน้มถ่วงของโลกก็เป็นแรงที่คอยรบกวนการเคลื่อนที่ของดาวเทียมเช่นกัน แรงโน้มถ่วงนี้จะคอยดึงดาวเทียมให้ต่ำลงเรื่อยๆจนเข้าสู่บรรยากาศโลก ซึ่งบรรยากาศโลกก็มีแรงต้านที่ทำให้ความเร็วของดาวเทียมลดลงเช่นกัน
สิ่งที่เราเคยเรียนและศึกษาเกี่ยวกับวงโคจร เราอาจเข้าใจได้ว่าการเคลื่อนที่รอบๆวัตถุใดๆในอวกาศจะอาศัยกฏการเคลื่อนที่ของเคปเลอร์ ซึ่งการเคลื่อนที่ของดาวเทียมที่โคจรอยู่รอบโลกก็อาศัยกฏของเคปเลอร์นี่แหละครับ แต่ว่า!!! มันไม่ได้สมบูรณ์แบบขนาดนั้นครับ
เพราะอะไร....เพราะสัณฐานของโลกครับ สัณฐานโลกไม่ได้เป็นทรงกลมสมบูรณ์เพอร์เฟคอะไรขนาดนั้นครับ มันมีลักษณะเป็นทรงกลมแป้น โดยมีความป่องออกบริเวณศูนย์สูตร อันเนื่องมาจากการหมุนรอบตัวเองของโลกซึ่งสร้างแรงหนีศูนย์กลาง ทำให้รัศมีที่เส้นศูนย์สูตรของโลกมีขนาดใหญ่กว่ารัศมีที่ขั้วโลกประมาณ 21 กิโลเมตร และนี่เป็นเหตุให้เกิดผลกระทบต่อวงโคจร ผลกระทบนั้นคือ Earth Second Zonal Harmonic หรือ J2 Perturbations 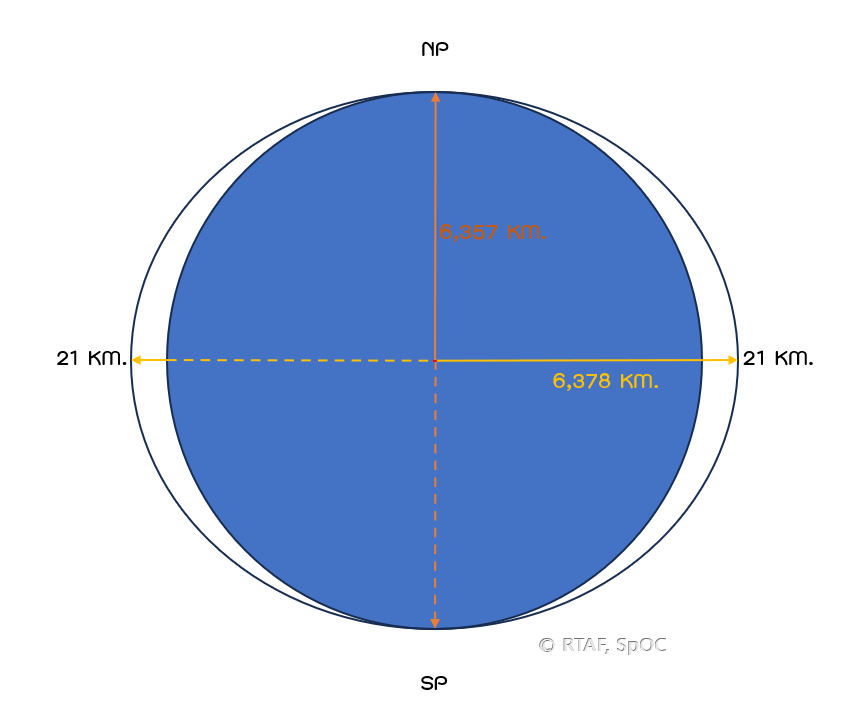
รูปที่ 1 : แสดงความยาวรัศมีของโลกบริเวณเส้นศูนย์สูตร
องค์ประกอบหลักสองอย่างของวงโคจรที่ได้รับผลกระทบจากการรบกวนของ J2 ได้แก่ การเปลี่ยนแปลงของตำแหน่งโหนดขาขึ้น RAAN (Ω) และ Argument of Perigee (ω) หากเราจำลองโลกเป็นทรงกลมสมบูรณ์ที่มีสนามโน้มถ่วงสม่ำเสมอ RAAN และ Argument of Perigee จะไม่มีการเปลี่ยนแปลง แต่เนื่องจากโลกของเราไม่ใช่ทรงกลมสมบูรณ์ นี่จึงเป็นสิ่งสำคัญที่เราต้องคำนึงถึงผลกระทบที่เกิดจากการรบกวนนี้ครับ
การรบกวนนี้ส่งผลอย่างไรกับค่า RAAN (Ω)
การรบกวนนี้สร้างผลกระทบที่แตกต่างกันออกไปในแต่ละระนาบวงโคจรที่มีค่า Inclination แตกต่างกันครับ โดยที่
เมื่อค่า i > 90 องศา หรือ วงโคจรแบบ Retrograde อัตราการบิดตัวของวงโคจรจะไปทาง Right Ascension คือมีการบิดตัวไปทางทิศตะวันออก ผลกระทบนี้แหละครับที่ถูกนำมาใช้กับวงโคจรแบบสัมพันธ์กับดวงอาทิตย์ หรือ Sun-Synchronous Orbit ถ้าอยากรู้ว่า วงโคจรแบบสัมพันธ์กับดวงอาทิตย์คืออะไร ลองเข้าไปอ่านได้ที่ "Sun-Synchronous วงโคจรที่อาศัยความไม่สมบูรณ์"
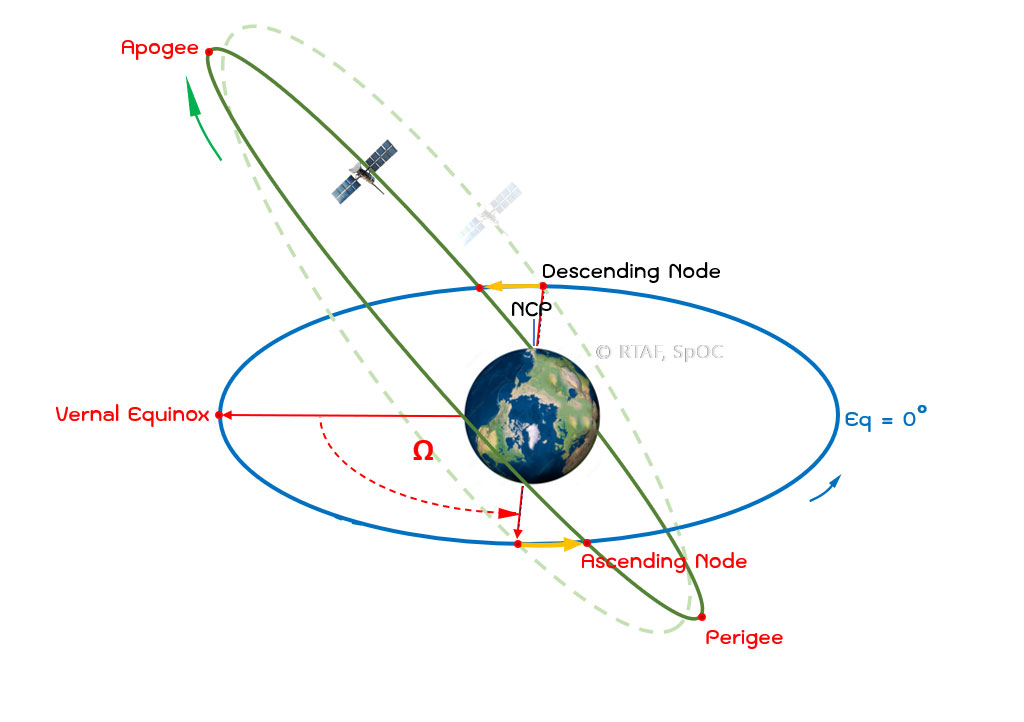
รูปที่ 2 : ลูกศรสีส้มแสดงการบิดตัวของระนาบวงโคจรไปทางทิศตะวันออก
เมื่อค่า 0 < i < 90 องศา หรือวงโคจรแบบ Prograde อัตราการบิดตัวของวงโคจรจะลดไปทางทิศตะวันตก
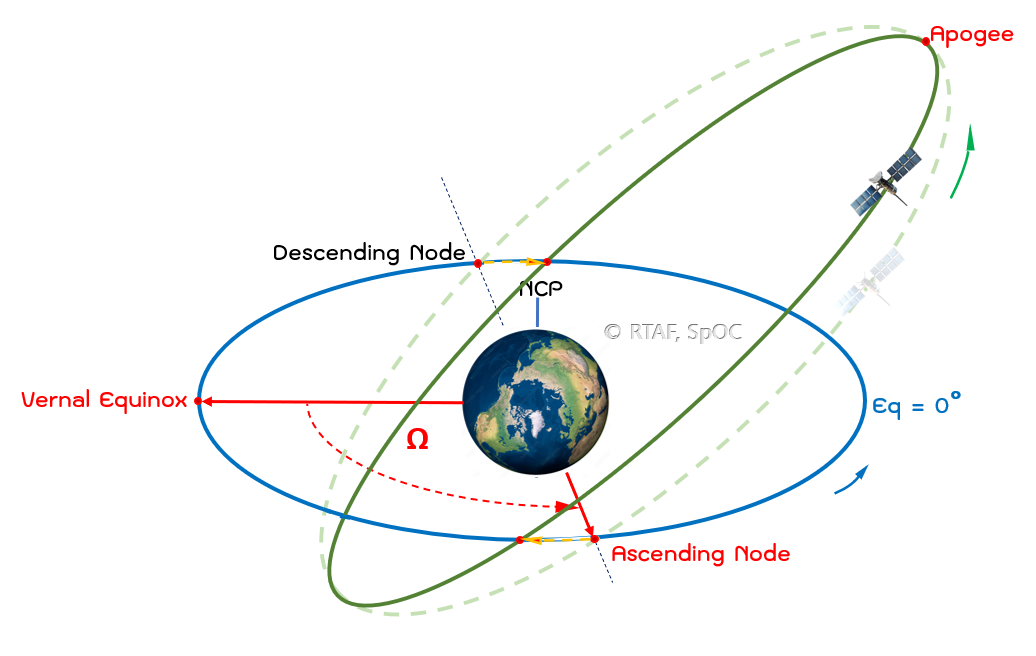
รูปที่ 3 : ลูกศรสีส้มแสดงทิศทางการบิดระนาบวงโคจรไปทางทิศตะวันตก
เมื่อค่า i = 0 และ 180 องศา ในกรณีนี้ เป็นระนาบวงโคจรที่มี อัตราการบิดตัวสูงที่สุดครับ แต่ทิศทางการบิดตัวจะแตกต่างกันตรงที่
ถ้า i = 0 องศา (Prograde) ระนาบการบิดตัวของวงโคจรจะลดลง โดยเคลื่อนที่ไปทางตะวันตก ส่งผลให้ดาวเทียมจะเคลื่อนที่ตามหลังดวงอาทิตย์ไปเรื่อยๆในแต่ละวัน ทำให้เวลาท้องถิ่นที่ดาวเทียมเคลื่อนที่ผ่านจะเร็วขึ้นในทุกๆวัน เช่น ดาวเทียมผ่านประเทศไทยในเวลา 10 โมงเช้าในวันนี้ และในวันรุ่งขึ้นดาวเทียมจะผ่านประเทศไทยเวลา 8 โมงเช้า
ถ้า i = 180 องศา (Retrograde) ระนาบการบิดตัวของวงโคจรจะเพิ่มขึ้น โดยเคลื่อนที่ไปทางตะวันออก ส่งผลให้ดาวเทียมเคลื่อนที่นำหน้าดวงอาทิตย์ไปเรื่อยๆในแต่ละวัน ทำให้เวลาท้องถิ่นที่ดาวเทียมเคลื่อนที่ผ่านจะช้าลงในทุกๆวัน
เมื่อค่า i = 90 องศา หรือวงโคจรแบบ Polar Orbital เป็นวงโคจรที่เคลื่อนที่ในแนว เหนือ-ใต้ ซึ่งวงโคจรแบบนี้ไม่ได้รับผลกระทบใดๆเลยจาก J2 Perturbations เนื่องจากระนาบการโคจรที่ทำมุมตั้งฉากกับระนาบศูนย์สูตรพอดี แรงที่กระทำต่อระนาบวงโคจรจึงสมดุลกัน (i > 90 องศา : ระนาบบิดไปทางตะวันออก, i < 90 องศา : ระนาบบิดไปทางตะวันตก) ทำให้เกิดแรงลัพธ์สุทธิที่ทำให้การบิดตัวของระนาบวงโคจรเป็นศูนย์
ทั้งหมดที่ผมกล่าวมานี้เป็นแค่ผลกระทบที่เกิดขึ้นกับค่า RAAN เท่านั้นครับ จะเห็นได้ว่าแค่การบิดตัวของ RAAN ก็ส่งผลกระทบต่อการใช้งานดาวเทียมแล้วครับ ซึ่งยังมีผลกระทบที่เกิดกับ Argument of Perigee (ω) อีก
การรบกวนที่ส่งผลกระทบต่อ Argument of Perigee (ω)
ผลกระทบที่เกิดขึ้นกับ Argument of Perigee คือการหมุนของระนาบวงโคจร (อย่าสับสนนะครับ กรณีของ RAAN เป็นการบิดตัวของระนาบวงโคจรบนระนาบศูนย์สูตร แต่สำหรับ Argument of Perigee เป็นการหมุนของระนาบวงโคจรครับ หรือมองว่าเป็นการหมุนของวงรีก็ได้ครับ ซึ่งส่งผลให้ Ascending Node กับ Descending Node เปลี่ยนตำแหน่งบนระนาบวงโคจร) ซึ่งทำให้ค่า (ω) มีการเพิ่มขึ้นหรือลดลง ส่งผลต่อการเปลี่ยนตำแหน่ง Perigee และ Apogee ของวงโคจรบนทรงกลมท้องฟ้า
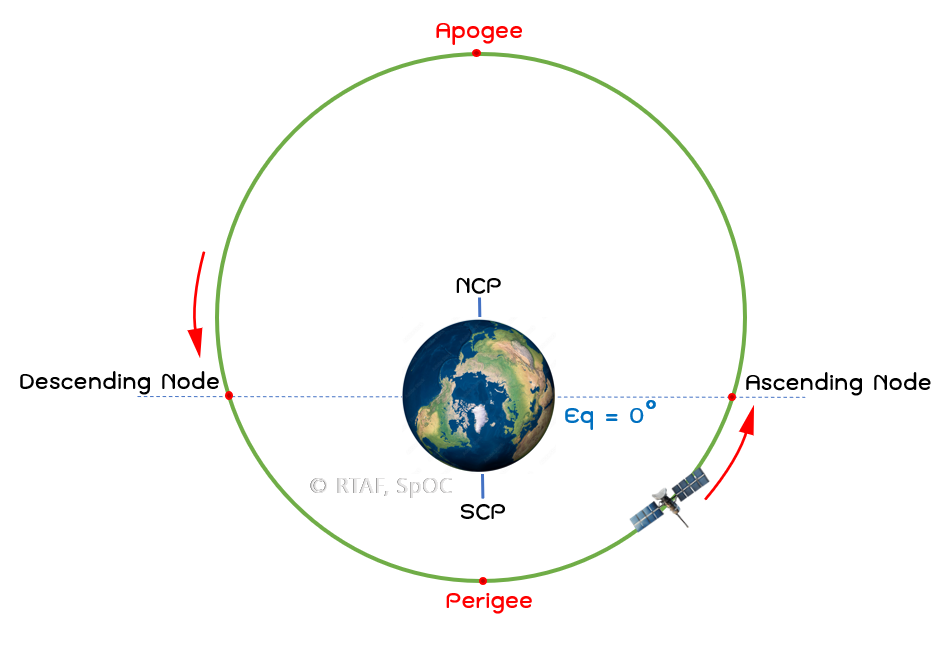
รูปที่ 4 : ทิศทางของแรงดึงบริเวณศูนย์สูตรที่ส่งผลกระทบต่อตำแหน่ง Perigee
ความไม่สมมาตรของแรงที่เกิดจากการป่องออกของโลกบริเวณเส้นศูนย์สูตร ทำให้เมื่อเวลาดาวเทียมเคลื่อนที่ผ่านแรงโน้มถ่วงส่วนเกิน จะมีแรงดึงดาวเทียมให้เคลื่อนที่เข้าหาระนาบศูนย์สูตร เช่น เมื่อดาวเทียมเคลื่อนที่อยู่เหนือระนาบศูนย์สูตร แรง J2 จะดึงดาวเทียมเข้าใกล้ระนาบศูนย์สูตรโดยมุ่งไปทางใต้ ซึ่งจะเป็นเช่นเดียวกันกับเมื่อดาวเทียมอยู่ต่ำกว่าระนาบศูนย์สูตร นอกจากแรงนี้จะพยายามทำให้ระนาบวงโคจรของดาวเทียมกลับไปทับกับระนาบของศูนย์สูตรจนทำให้เกิดการบิดตัว (Precession) แล้วนั้น แรงดึงนี้จะทำให้วงโคจรที่เป็นวงรีถูกยืดหรือขยายออกไปตามแนวที่ตั้งฉากกับแรง ส่งผลให้ตำแหน่ง Perigee มีการขยับเลื่อนตำแหน่งออกไปจากเดิมบนระนาบวงโคจร ซึ่งผลกระทบที่เกิดขึ้นกับ Argument of perigee นั้นแตกต่างไปจากค่า Inclination ของแต่ละวงโคจรโดยที่
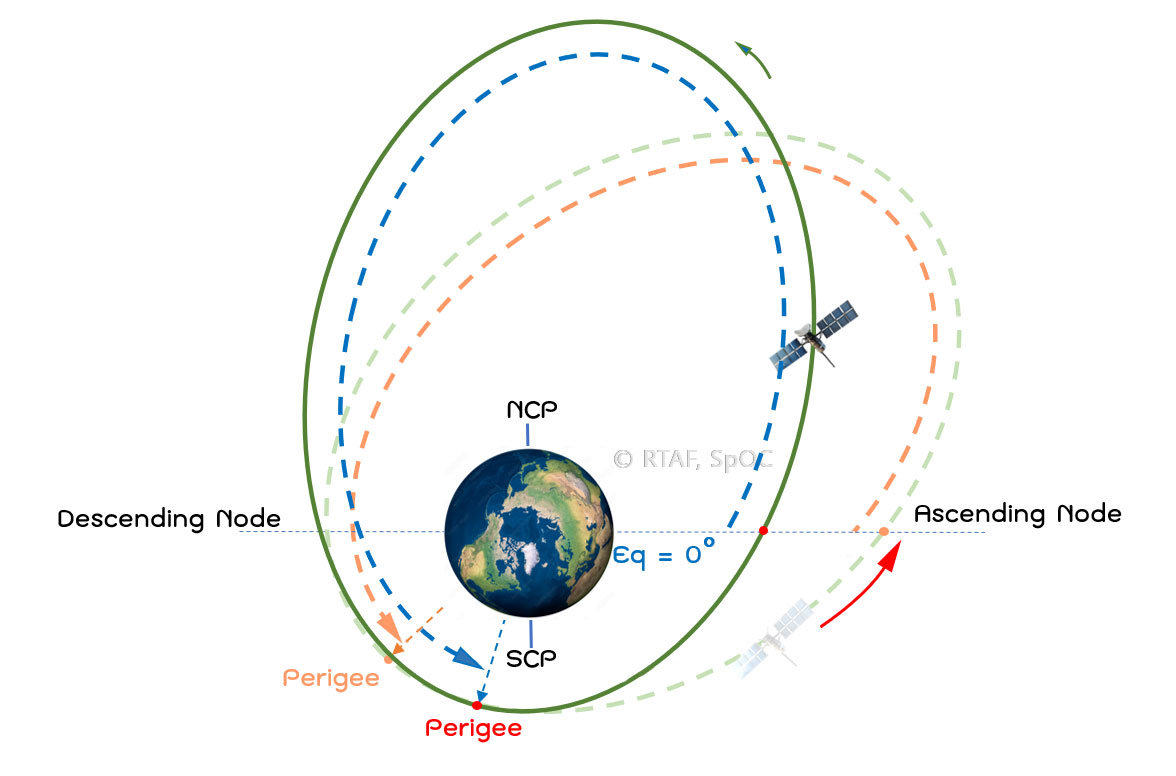
รูปที่ 5 : แสดงการเปลี่ยนตำแหน่งของ Perigee จนส่งผลต่อค่า Argument of Perigee ที่เพิ่มขึ้น
เมื่อมุม 0 < i < 63 องศา และ มุม 116 < i < 180 องศา ทิศทางการหมุนของ Perigee จะเลื่อนไปข้างหน้า ซึ่งทำให้ค่ามุม Argument of Perigee (ω) เพิ่มขึ้น
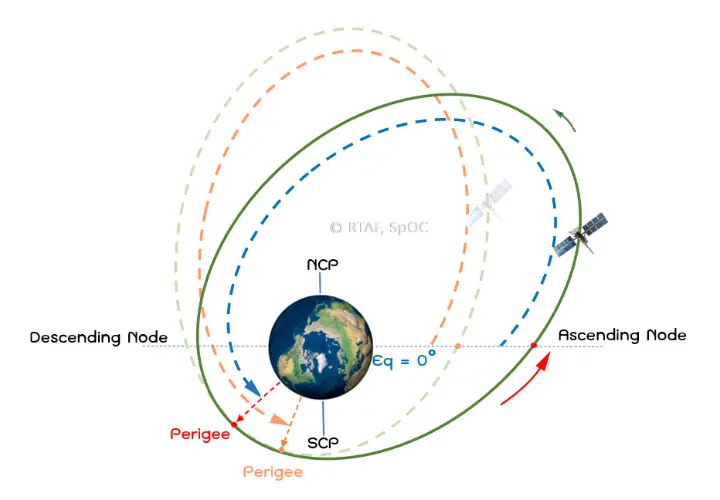
รูปที่ 6 : แสดงการเปลี่ยนตำแหน่งของ Perigee จนส่งผลต่อค่า Argument of Perigee ที่ลดลง
เมื่อมุม 63 < i < 116 องศา ทิศทางการหมุนของ Perigee จะเลื่อนไปข้างหลัง ซึ่งทำให้ค่ามุม Argument of Perigee (ω) ลดลง
เมื่อมุม i = 63 และ 116.6 องศา ทิศทางการหมุนของ Perigee จะไม่เปลี่ยนแปลง ซึ่งถูกใช้ในการออกแบบวงโคจรแบบ Molniya ที่มีความเยื้องศูนย์กลางของวงโคจรมาก เนื่องจาก J2 ไม่มีผลกระทบต่อการเปลี่ยนตำแหน่งของ Perigee นั่นก็แปลว่า Apogee ไม่มีการเปลี่ยนแปลงเช่นกัน การออกแบบนี้ก็เพื่อรักษาระยะเวลาให้ ตำแหน่ง Apogee อยู่เหนือพื้นที่ซีกโลกใดซีกโลกหนึ่งได้นานๆ
การรบกวนที่ส่งผลกระทบต่อ Mean Anomaly (M)
เราอาจจะไม่คุ้นคำว่า Mean Anomaly เพราะเราไม่เห็นมันอยู่ในองค์ประกอบวงโคจร แต่มันเป็นค่าที่ออกแบบมาให้เป็นฟังก์ชันเชิงเส้นของเวลา ในการคำนวณความเร็วเชิงมุมเฉลี่ยของวัตถุที่โคจรครบ 1 รอบ ผลกระทบที่เกิดขึ้นจากการรบกวน จึงส่งผลกับเวลาที่ใช้ในการโคจรครบ 1 รอบ ยกตัวอย่างเช่น ดาวเทียมโคจรผ่านตำแหน่งหนึ่งของประเทศไทย ใน 1 รอบที่ดาวเทียมโคจรผ่าน ใช้เวลา 90 นาที ผลกระทบจาก J2 Perturbations นี้ ส่งผลให้ Mean Motion เปลี่ยนไป คือ คาบการโคจรจะมีการเปลี่ยนไป 1-2 วินาที หากสะสมไปเรื่อยๆในแต่ละรอบ ความแม่นยำต่อภารกิจในการถ่ายภาพจะน้อยลง เพราะดาวเทียมจะมีตำแหน่งเคลื่อนที่ออกจากจุดเดิมที่เคยคาดการณ์ไว้
การโคจรของดาวเทียมหากเป็นไปตามกฏของเคปเลอร์ทั้งหมด มันก็ไม่ได้มีอะไรซับซ้อน และคงง่ายมากขึ้นที่จะใช้สำหรับติดตามตำแหน่งของวัตถุอวกาศที่โคจรอยู่รอบโลก แต่ในความเป็นจริง มันไม่ใช่อย่างที่คิดเลยครับ ปัจจัยหลายๆอย่างซึ่งมากกว่าที่ผมอธิบายมา ก็เป็นปัจจัยที่ส่งผลกระทบต่อวงโคจรเช่นกัน การติดตามวัตถุในวงโคจรต่างๆ จึงจำเป็นต้องอาศัยข้อมูลจากเซนเซอร์และอัลกอริทึม ในการคำนวณเพื่อคาดการณ์วิถีการโคจรอยู่ตลอดเวลา

บทความโดย
ร.ท.เอกพล ไพบูลย์นภาพงศ์