สวัสดีครับสำหรับท่านที่เข้ามาอ่านบทความหัวข้อนี้ บางท่านอาจจะเคยทราบองค์ประกอบของวงโคจร หรือ เรียกว่า Orbital Elements มาบ้างแล้วว่าประกอบไปด้วยอะไรบ้าง เราลงมาทบทวนกันก่อนละกันครับ
1. Semi-major axis (a) : เป็นองค์ประกอบที่กล่าวถึงระยะครี่งหนึ่งของแกนเอก ทำไมถึงเรียกว่าแกนเอก มันมีมากกว่า 1 แกนหรอ!! ใช่ครับ วงโคจรของวัตถุไม่ได้เป็นวงกลม แต่มันมีลักษณะเป็นวงรีครับ ดังนั้นค่า (a) จึงเป็นค่าที่สามารถบ่งบอกถึงขนาดของวงโคจร (Size of Orbit), ระยะทางเฉลี่ย (Average Distance) ระหว่างวัตถุที่โคจรกับวัตถุศูนย์กลางของการโคจร และ คาบการโคจร (Orbital Period) ซึ่งมีความสัมพันธ์โดยตรงกับระยะครึ่งหนึ่งของแกนเอก (a) เลยครับ โดยสามารถอธิบายได้ตาม กฏข้อที่ 3 ของ โยฮันเนส เคปเพลอร์ ที่ระบุว่า คาบในการโคจรกำลังสองแปรผันตรงกับระยะครึ่งแกนเอกของวงโคจรกำลังสาม
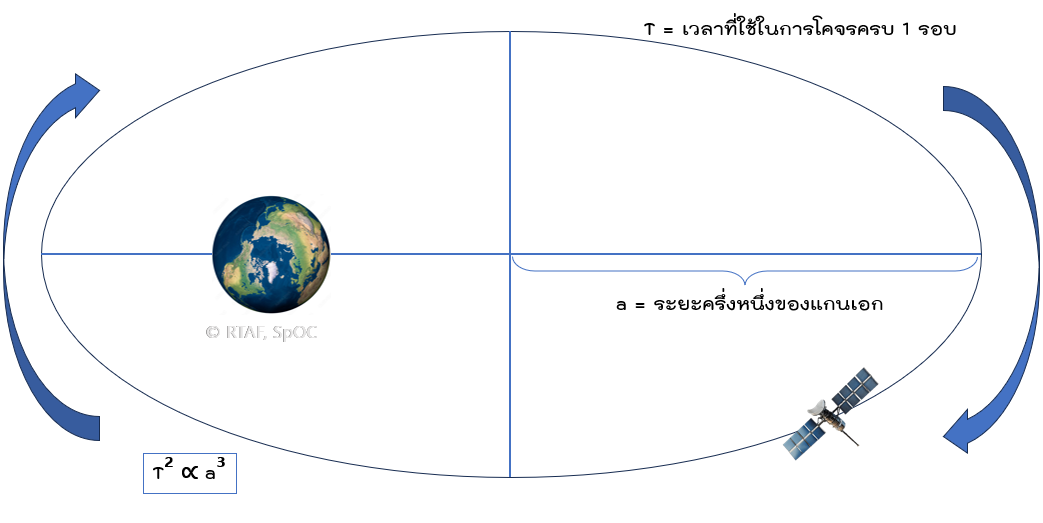
รูปที่ 1 : คาบในการโคจรกำลังสองแปรผันตรงกับระยะครึ่งแกนเอกของวงโคจรกำลังสาม
2. Eccentricity (e) : เป็นองค์ประกอบที่กล่าวถึงค่าความรีของวงโคจร โดยที่ e = 0 วงโคจรจะเป็นวงกลม และ ถ้า 0<e<1 วงโคจรจะเป็นวงรี ถ้าอธิบายในเชิงคณิตศาสตร์ มันคือค่าที่บ่งบอกถึงรูปร่างของภาคตัดกรวยนั่นเองครับ หากเราพิจารณาถึงค่า e แล้วเราจะทราบว่ามันเป็นตัวบ่งบอกว่าระยะใกล้สุด (Perigee) และระยะไกลสุด (Apogee) ว่ามีผลต่างกันมากน้อยแค่ไหน
อ่อ!!! บางท่านอาจจะสงสัยว่า เป็นไปได้ไหมที่วงโคจรจะเป็นวงกลมสมบูรณ์โดยที่มีค่า Perigee และ Apogee ที่แตกต่างกัน ตอบว่า เป็นไปไม่ได้ครับ เพราะวงกลมสมบูรณ์ค่าความเยื้องศูนย์กลางจะเป็น 0 ในทันที หากมีระยะใกล้ไกลที่แตกต่างกัน จุดศูนย์กลางของแรงจะไม่ใช่ตำแหน่งเดียวกันซึ่งนั่นเป็นไปไม่ได้ตามคุณสมบัติของวงกลมที่มีจุดศูนย์กลางเพียงจุดเดียวครับ
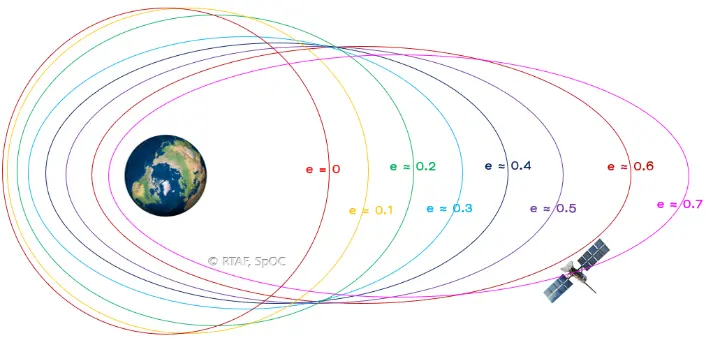
รูปที่ 2 : แสดงถึงค่า e ของวงโคจร
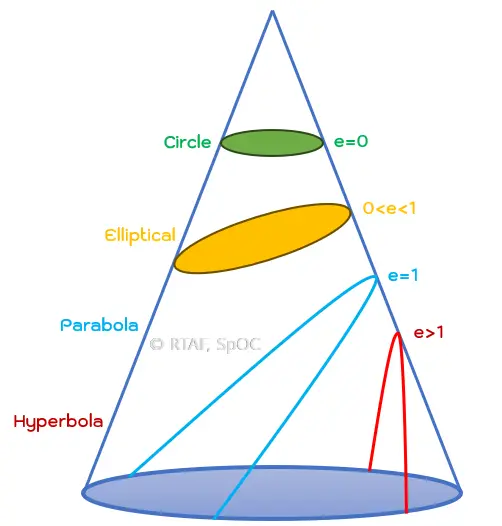
รูปที่ 3 : แสดงภาคตัดกรวยในแต่ละระนาบ
3. Inclination (i) : (และนี่คือหัวข้อหลักของบทความนี้ เดี๋ยวผมจะอธิบายองค์ประกอบของวงโคจรให้ครบก่อนละกันครับ แล้วเราค่อยมาคุยกันถึงค่า (i)) เป็นองค์ประกอบที่กล่าวถึงมุมเอียงของระนาบวงโคจรของวัตถุกับระนาบอ้างอิงที่เส้นศูนย์สูตร และทิศทางการโคจร โดยมีค่าอยู่ระหว่าง 0 - 180 องศา
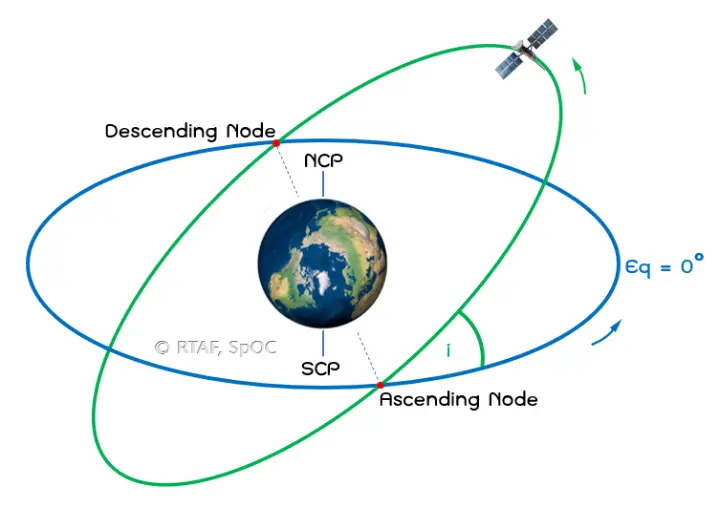
รูปที่ 4 : อธิบายค่า Inclination ของวงโคจรเมื่อเทียบกับระนาบอ้างอิงศูนย์สูตรโลก
ค่า i = 0 องศา แบบนี้เรียกว่า Equatorial Orbit คือ วัตถุมีวงโคจรไปในทิศทางเดียวกับการหมุนของโลกโดยวางตัวอยู่บนระนาบศูนย์สูตร หากอยู่บนความสูงที่ 35,786 กิโลเมตรเหนือพื้นโลก วัตถุนี้จะเหมือนลอยค้างฟ้าไม่ขยับไปไหน โดยมีคาบการโคจรเท่ากับเวลาที่โลกหมุนรอบตัวเอง (ประมาณ 24 ชั่วโมง)
ค่า 0 < i < 90 องศา แบบนี้เรียกว่า Prograde Orbit คือ วัตถุมีวงโคจรไปในทิศทางเดียวกับการหมุนของโลกแต่มีวงโคจรที่ตัดกับระนาบศูนย์สูตร 2 ตำแหน่ง โดยตำแหน่งที่วัตถุเคลื่อนที่จากทิศใต้ขึ้นไปทิศเหนือ จุดตัดของระนาบวงโคจกับระนาบศูนย์สูตรจะถูกเรียกว่า โหนดขาขึ้น (Ascending Node) และตำแหน่งที่วัตถุเคลื่อนที่จากทิศเหนือไปทิศใต้ จุดตัดของระนาบวงโคจกับระนาบศูนย์สูตรจะถูกเรียกว่า โหนดขาลง (Descending Node)
ค่า 90 < i < 180 องศา แบบนี้เรียกว่า Retrograde Orbit คือ วัตถุมีวงโคจรในทิศที่ตรงข้ามกับการหมุนของโลก มีจุดตัดของระนาบวงโคจรกับระนาบอ้างอิง (Equatorial Plane) 2 ตำแหน่งเช่นเดียวกัน
4.
Right Ascension of Ascending Node (Ω) : เป็นองค์ประกอบที่กล่าวถึงมุม โดยบ่งบอกถึงทิศทางของระนาบวงโคจรเมื่อเทียบกับระนาบอ้างอิง อ่านมาตรงนี้บางท่านอาจจะงงว่า แล้วมันต่างกันอย่างไรกับค่า Inclination อธิบายอย่างนี้ครับ ค่า RAAN เป็นเหมือนการกำหนดเส้น Longitude สมมุติบนทรงกลมฟ้าว่าระนาบการโคจรของวัตถุนั้นตัดกับ Longitude สมมุติ ใด ณ เวลาที่ถูกกำหนด ลองนึกภาพว่าวัตถุกำลังโคจรรอบแกน Z ที่ชี้ไปยังตำแหน่ง Vernal Equinox ซึ่งมีค่า RA, Dec = 0 องศา หลังจากนั้นเราจะทำการวัดมุมจากแกน Z ไปที่ตำแหน่ง Ascending Node (ตำแหน่งโหนดขาขึ้นที่ระนาบวงโคจรตัดกับระนาบศูนย์สูตร) ค่ามุมที่ได้ก็คือ RAAN หรือ Right Ascension of Ascending Node (Ω) นั่นเอง
(Vernal Equinox คือจุดตัดกันระหว่างระนาบสุริยวิถี Ecliptic Plane (ระนาบสุริยวิถี : มันคือระนาบที่เราสมมุติว่าดวงอาทิตย์เคลื่อนที่รอบโลก แต่จริงๆแล้วมันคือระนาบที่โลกเนี่ยะแหละโคจรรอบดวงอาทิตย์) กับระนาบศูนย์สูตรโลก เป็นตำแหน่งบนทรงกลมฟ้าที่ Right Ascension และ Declination เท่ากับ 0 องศา ตำแหน่งนี้จะชี้ไปที่กลุ่มดาวปลา (กลุ่มดาวประจำราศีมีน) Vernal Equinox จึงเกิดขึ้นประมาณวันที่ 21 มีนาคม ของทุกปี เป็นวันที่ระนาบศูนย์สูตรโลกทำมุม 0 องศากับแสงอาทิตย์ ส่งผลให้เวลากลางวันเท่ากับเวลากลางคืน ปรากฏการนี้จะเกิดขึ้นอีก 6 เดือนข้างหน้า คือประมาณ วันที่ 21 ก.ย. เรียกว่า Autumnal Equinox)
สรุปคือ Inclination (i) คือค่ามุม Elevation ที่วัดจากระนาบศูนย์สูตร ส่วน RAAN (Ω) คือค่ามุม Azimuth ของวงโคจรบนระนาบศูนย์สูตรที่วัดจากจุด Vernal Equinox นั่นเอง มุม RAAN นี้จะมีการบิดตัวอยู่ตลอดจากการรบกวนของ Earth Second Zonal Harmonic
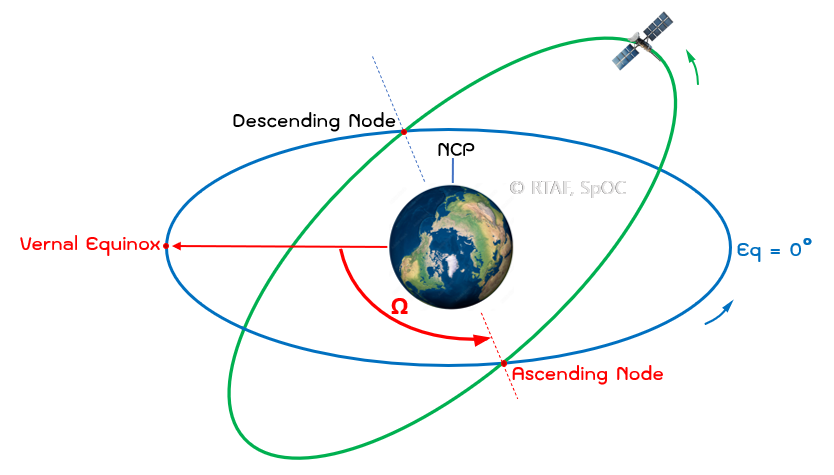
รูปที่ 5 : อธิบายมุม RAAN เมื่อวัดจากตำแหน่ง Vernal Equinox ถึง Ascending Node
5. Argument of Perigee (ω) : เป็นองค์ประกอบที่กล่าวถึงมุมอีกเช่นกันครับ โดยเป็นค่ามุมที่วัดจาก โหนดขาขึ้น (Ascending Node) ไปสิ้นสุดที่ตำแหน่ง Perigee ทำให้เราทราบว่า แกนหลักของวงรี(วงโคจร)วางตัวอยู่ในทิศทางใดในระนาบนั้นๆ เช่น
ω = 0 องศา หมายความว่า จุดใกล้สุดของวัตถุที่โคจรรอบโลก (Perigee) จะอยู่ที่ตำแหน่ง โหนดขาขึ้น (Ascending Node)
ω = 90 องศา หมายความว่า จุดใกล้สุดของวัตถุที่โคจรรอบโลก (Perigee) จะอยู่ที่ตำแหน่งเหนือเส้นศูนย์สูตร (แต่จะอยู่เหนือ Latitude เท่าไหร่ขึ้นอยู่กับค่า (i))
ω = 180 องศา หมายความว่า จุดใกล้สุดของวัตถุที่โคจรรอบโลก (Perigee) จะอยู่ที่ตำแหน่ง โหนดขาลง (Descending Node) นั่นหมายความว่า จุดไกลสุดของวัตถุที่โคจรรอบโลก (Apogee) จะอยู่ที่ตำแหน่งเดียวกันกับโหนดขาขึ้น (Ascending Node) นั่นเอง
ω = 270 องศา หมายความว่า จุดใกล้สุดของวัตถุที่โคจรรอบโลก (Perigee) จะอยู่ตำแหน่งต่ำสุดจากระนาบศูนย์สูตร (ซีกโลกใต้) จุดไกลสุดของวัตถุที่โคจรรอบโลก (Apogee) จะอยู่ตำแหน่งสูงสุดของระนาบศูนย์สูตร (ซีกโลกเหนือ) ดังแสดงในรูปที่ 6
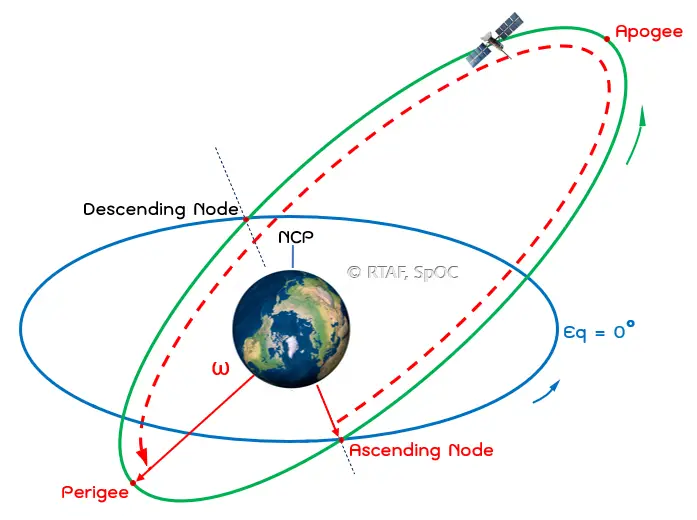
รูปที่ 6 : อธิบายมุม ω โดยการวัดจากตำแหน่ง Ascending Node ถึง ตำแหน่ง Perigee
ตำแหน่ง Perigee มีความสำคัญต่อการเปลี่ยนวงโคจรของวัตถุ เพราะเป็นตำแหน่งที่วัตถุมีความเร็วสูงสุดเพราะอยู่ใกล้โลก การจุดเชื้อเพลิงเพื่อสร้างแรงขับในทิศทางเดียวกันกับการโคจร ณ ตำแหน่งนี้จะประหยัดเชื้อเพลิงมากที่สุด และก็เช่นกันครับ ตำแหน่ง Apogee ก็มีความสำคัญในการเปลี่ยนวงโคจรเช่นกัน อย่างเช่น การเปลี่ยนวงโคจรในการนำส่งดาวเทียม GEO จะเริ่มจากวงโคจร GTO (Geo Transfer Orbit) ซึ่งมีค่า Apogee ที่สูง และ Perigee ที่ต่ำ การจะปรับให้ค่า Perigee สูงขึ้น จะต้องจุดเชื้อเพลิง ณ ตำแหน่ง Apogee ในทิศทางเดียวกันกับวิถีการโคจร
(นิดนึงครับ!!! การนำส่งดาวเทียมในวงโคจร GEO เนี้ยะมันไม่ใช่การยิงจรวดขึ้นไปจนถึง 35,786 กิโลเมตรนะครับ แต่เป็นการนำส่งไปที่วงโคจรแบบ LEO แล้วทำการ Transfer ตำแหน่งขึ้นไปเรื่อยๆด้วยแรงหนีศูนย์กลางและวิธีการปรับแต่งแรงขับบริเวณจุด Apogee และ Perigee การใช้แรงขับที่ถูกตำแหน่งจะช่วยทำให้มีการใช้เชื้อเพลิงอย่างมีประสิทธิภาพ ลองนึกภาพตอนเราไกวชิงช้าอ่ะครับ แต่มันต้องแลกมาด้วยระยะเวลาประมาณ 4-5 เดือนหลังการนำส่งกว่าที่ดาวเทียมจะสามารถเข้าประจำตำแหน่งที่ต้องการได้)
ในการรักษาระดับความสูงของดาวเทียมโดยเฉพาะ วงโคจรต่ำ (Low Earth Orbit) การรักษาระดับความสูงของวงโคจรก็จะใช้วิธีเพิ่มความเร่งที่ตำแหน่ง Apogee เพื่อตรึงความสูงของ Perigee ไว้ครับ
6. True Anomaly (v) : เป็นองค์ประกอบสุดท้าย แต่ก็ยังกล่าวถึงมุมอยู่ดีครับ เป็นค่ามุมที่วัดจากตำแหน่ง Perigee ไปยังตำแหน่งตำแหน่งปัจจุบันของวัตถุ โดยมุมนี้อยู่บนระนาบวงโคจรของวัตถุนั้นๆ และมีจุดยอดของมุมอยู่ที่ศูนย์กลางของวงโคจร เช่น โลก True Anomaly (v) มีค่าตั้งแต่ 0-360 องศา โดยที่
v = 0 องศา หมายความว่า วัตถุอยู่ที่ตำแหน่ง Perigee ซึ่งเป็นตำแหน่งที่วัตถุมีความเร็วสูงสุดในการโคจร
v = 180 องศา หมายความว่า วัตถุอยู่ที่ตำแหน่ง Apogee ซึ่งเป็นตำแหน่งที่วัตถุมีความเร็วต่ำสุดในการโคจร
v = 90 หรือ 270 หมายความว่า วัตถุอยู่ที่ตำแหน่ง ด้านข้างของวงโคจร (บริเวณแนวเส้น Minor Axis ของวงโคจร)
True Anomaly เป็นองค์ประกอบในวงโคจรที่ไม่ปรากฏอยู่ใน TLE (Two-Line Elements) เนื่องจากวงโคจรที่เป็นแบบวงกลมค่า True Anomaly จะเพิ่มด้วยความเร็วคงที่ แต่ในความเป็นจริง วงโคจรของวัตถุเป็นวงรี วัตถุจึงไม่ได้เคลื่อนที่ด้วยความเร็วเชิมมุมที่คงที่ตลอดระนาบการโคจร ค่าที่ปรากฎใน TLE จึงเป็น Mean Anomaly ค่านี้เป็นมุมที่เทียบกับเวลาในคติที่วงโคจรเป็นวงกลมสมบูรณ์ครับ มันใช้บอกว่า ณ เวลาที่ Epoch Time วัตถุอยู่ตำแหน่งใดในวงโคจร เช่น Mean Anomaly = 0.000 หมายถึงวัตถุอยู่ ณ ตำแหน่ง Perigee ที่เวลา Epoch Time
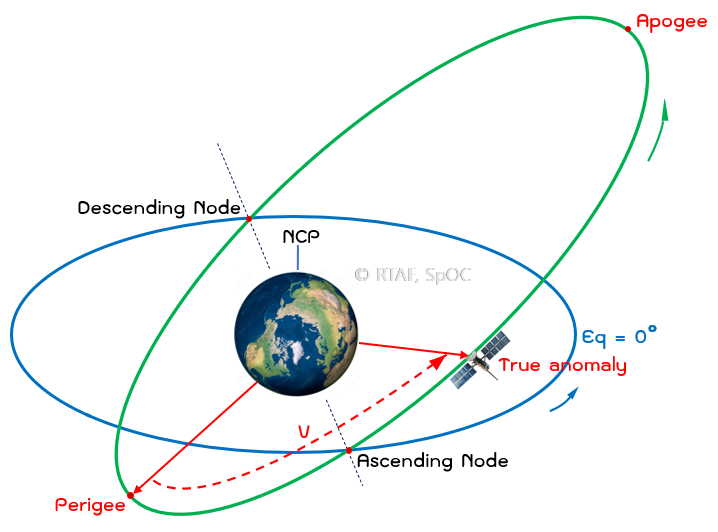
รูปที่ 7 : อธิบายมุม True Anomaly โดยวัดตำแหน่งจาก Perigee ถึง ตำแหน่งปัจจุบันของดาวเทียม บนระนาบวงโคจร
อ่านมาถึงตรงนี้ แล้วพักดื่มน้ำ ทำธุระส่วนตัวก่อนละกันครับแล้วค่อยกลับมาอ่านต่อ
คราวนี้ก็ถึงประเด็นหัวข้อที่ผมกล่าวมาข้างต้นแล้วนั่นคือ Inclination หนึ่งในองค์ประกอบของวงโคจรที่เราต้องรู้ จริงๆแล้วองค์ประกอบของวงโคจรเป็นสิ่งที่เราต้องรู้ทั้งหมดแหละครับ ขาดอย่างใดอย่างหนึ่งไม่ได้ แต่ที่ผมจะพูดถึง Inclination เพราะมันเป็นองค์ประกอบที่เราควรทราบตั้งแต่ต้นว่า ดาวเทียมของเราที่จะถูกนำส่งขึ้นไปนั้น มันมี Inclination เท่าไหร่ และควรมี Inclination เท่าไหร่ เพราะ!!
1. Inclination มีผลต่อภารกิจของดาวเทียม
ผมไม่ขออธิบายเพิ่มเติมเกี่ยวกับค่า Inclination แล้วละกันครับ แต่จะกล่าวในลักษณะของการใช้งาน ของค่า Inclination ของดาวเทียมแต่ละประเภท
ดาวเทียมสื่อสารวงโคจรประจำที่ : เป็นดาวเทียมที่ใช้ค่า Inclination อยู่ที่ประมาณ 0 องศา จากระนาบศูนย์สูตร (ความสูง 35,786 กิโลเมตร) ผลที่ได้คือ ดาวเทียมจะลอยค้างฟ้าอยู่ ณ ตำแหน่งเดิมเหนือพื้นโลก เหมาะสำหรับให้บริการสื่อสารในระยะทางที่ไกลเช่นการสื่อสารข้ามทวีป
ดาวเทียมนำร่องวงโคจร GEO : .ในบัจจุบันมีบางประเทศที่พัฒนาดาวเทียมนำร่องขึ้นมาใช้งานเองโดยใช้วงโคจร GEO แต่ด้วยลักษณะทางภูมิศาสตร์ทำให้ไม่สามารถทำให้ดาวเทียมโคจรอยู่เหนือประเทศได้เช่น ญี่ปุ่น ซึ่งอยู่บริเวณ Latitude 20-45 องศาเหนือ จึงออกแบบวงโคจรของดาวเทียมให้มี Inclination ที่สูงประมาณ 40 องศา เพื่อให้ดาวเทียมมีวงโคจรในแนวเหนือใต้ และปรับค่า Apogee ให้สูงเหนือบริเวณ Latitude ของประเทศ เพื่อทำให้ดาวเทียมลอยค้างอยู่เหนือประเทศได้นานขึ้น ตัวอย่างเช่นดาวเทียมนำร่อง QZSS
ดาวเทียมสำรวจทรัพยากรณ์ EO : ดาวเทียมประเภทนี้จำเป็นต้องเคลื่อนที่ผ่านทุกๆบริเวณพื้นโลกให้มากที่สุด วงโคจรจึงจำเป็นต้องมีแนวระนาบ เหนือ-ใต้ เสมอ (เพราะโลกหมุนรอบตัวเองจากตะวันออกไปตะวันตก) แต่ด้วยดาวเทียมบางประเภทที่เป็น Optical จำเป็นต้องอาศัยแสงจากดวงอาทิตย์เป็นฉากหลังเพื่อไม่ให้เกิดเป็นเงามืดจากการถ่ายภาพ จึงจำเป็นต้องปรับค่า Inclination ประมาณ 98 องศา เพื่อให้ดาวเทียมผ่านตำแหน่งที่กำหนดในเวลาเดิมซ้ำๆทุกวัน เรียกวงโคจรประเภทนี้ว่า Sun-Synchronous Orbit
2. Inclination ทำให้เราเลือกตำแหน่งของจุดปล่อยจรวดนำส่ง
คืออย่างนี้ครับ ก่อนอื่นเราต้องเข้าใจลักษณะทางกายภาพของโลกเราก่อน โลกเรามีสัญฐานเป็นทรงกลมที่หมุนจากทิศตะวันตกไปทิศตะวันออก ถ้าอธิบายเชิงกลศาสตร์ทรงกลม วัตถุทรงกลมที่หมุนรอบตัวเองจะมีแรงเหวี่ยงหนีศูนย์กลาง โดยบริเวณที่มีแรงมากสุดคือเส้นแบ่งครึ่งทรงกลมที่อยู่ในระนาบเดียวกับทิศทางการหมุน ในที่นี้คือระนาบเส้นศูนย์สูตร
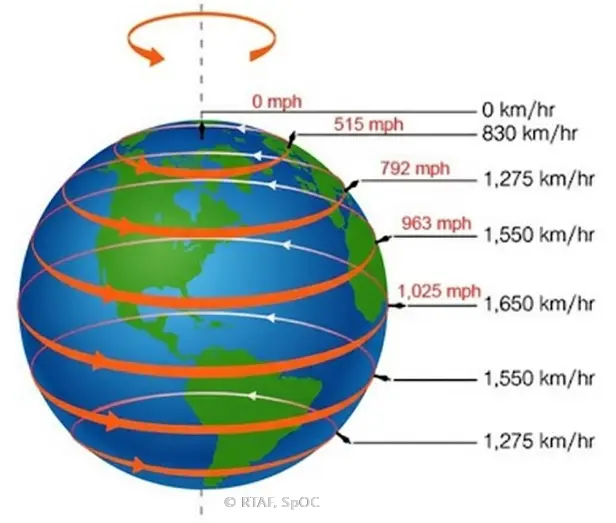
รูปที่ 8 : อธิบายค่า Velocity Surface ของแต่ละ Latitude บนผิวโลก
การยิงจรวดนำส่งดาวเทียมจากฐานยิงที่บริเวณระนาบศูนย์สูตรโดยการยิงไปทางทิศตะวันออก จะช่วยให้จรวดได้รับแรงเสริมจากการหมุนของโลก (Velocity Surface) ทำให้การใช้เชื้อเพลิงของจรวดมีประสิทธิภาพมากขึ้น ในขณะที่การยิงไปในทางทิศตะวันตก จรวดต้องสูญเสียเชื้อเพลิงมหาศาลเพื่อสร้างแรงขับขึ้นสู่บรรยากาศ (คล้ายๆการกระโดดลงจากรถแล้วหน้าทิ่ม)
จากผลลัพธ์ข้างต้น จะเห็นว่าการยิงจรวดจากตำแหน่งบริเวณศูนย์สูตรโลกเป็นตัวเลือกที่เหมาะสมที่สุดเพราะสามารถอาศัยแรงเสริมจากการหมุนของโลก แต่นั่นก็ไม่ใช่ว่าทุกประเทศจะมีฐานปล่อยจรวดที่อยู่บริเวณศูนย์สูตร ซึ่งก็ต้องไปแก้กันตอนปรับวงโคจรอ่ะเนอะ
ปัญหาอีกอย่างสำหรับฐานปล่อยจรวดใน Latitude อื่นคือ การปรับค่า Inclination หลังยิงจรวด เนื่องจาก ระนาบการโคจรของจรวดนำส่งจะผ่านจุดยิงเสมอ ทำให้การปรับ Inclination ที่มีองศาต่ำกว่า Latitude ที่ยิงเป็นไปไม่ได้เลยในทางปฏิบัติ ยกตัวอย่างเช่น ฐานยิงจรวดอยู่ที่ Latitude 40 องศา Inclination ต่ำสุดของจรวดที่จะทำได้คือ 40 องศาหรือมากกว่าจากการปรับมุมยิง (Launch Azimuth) ส่วนการยิงจรวดในระนาบ Polar Orbit สามารถยิงจาก Latitude ใดก็ได้ เนื่องจากเป็นการปรับมุมยิง (Launch Azimuth) ดังที่กล่าวมา แต่การยิงในที่ทิศที่ไม่ได้อยู่ในแนวการหมุนรอบตัวเองของโลก จรวดจะไม่ได้ประโยชน์จาก Earth Velocity เลย
หากยิงบริเวณ Latitude สูง และปรับให้จรวดมี Inclination ที่ต่ำกว่า Latitude ที่ยิง จรวดจำเป็นต้องใช้เชื้อเพลิงมหาศาลในการลดความเร็วเพื่อเปลี่ยนทิศทางและตำแหน่งเพื่อทำการปรับ Inclination ซึ่งไม่คุ้มค่าและสูญเสียเชื้อเพลิงไปโดยเปล่าประโยชน์ หรืออาจจะต้องนำเชื้อเพลิงขึ้นไปในปริมาณที่มากสำหรับใช้ปรับวงโคจร ซึ่งการหลีกเลี่ยงปัญหานี้คือการยิงจรวดจาก Latitude ที่ไม่สูงกว่าค่า Inclination
การปรับค่า Inclination ของดาวเทียมในกรณีที่ไม่สามารถกำหนดจุดของพื้นที่นำส่งได้ตามที่ต้องการ ก็มักจำเป็นต้องมีการปรับเมื่อวัตถุหรือดาวเทียมเริ่มเข้าสู่วงโคจร อย่างที่เคยกล่าวมานั่นแหละครับว่า Perigee และ Apogee เป็นจุดที่ใช้ปรับแต่งวงโคจรด้วยแรงขับ โดยเฉพาะตำแหน่ง Apogee ที่ความเร็วของดาวเทียมลดลง พลังงานที่ใช้ในการปรับแก้ก็จะน้อยลงเช่นกัน
ดังนั้นการนำส่งวัตถุที่มีระนาบวงโคจรใกล้แนวศูนย์สูตรจึงจำเป็นต้องยิงจรวดจากฐานยิงที่อยู่บริเวณแนวเส้นศูนย์สูตรให้มากที่สุด เพื่อลดการใช้เชื้อเพลิงที่ไม่เกิดประโยชน์และอาศัยประโยชน์จากการหมุนของโลก
จากบทความดังกล่าวจะเห็นว่า การรู้ภารกิจของดาวเทียมจะทำให้เราสามารถตัดสินใจได้ว่า Inclination ของดาวเทียมควรอยู่ที่เท่าไหร่ และนั่นทำให้เรารู้ว่าตำแหน่งของ Launch Site ควรเป็นที่ไหนบนโลก หวังว่าทุกท่านจะได้เกร็ดความรู้และประโยชน์จากบทความนี้ไม่มากก็น้อยนะครับ

บทความโดย
ร.ท.เอกพล ไพบูลย์นภาพงศ์